Variogram Analysis
Introduction
A variogram is a fundamental tool in geostatistics, used to quantify the spatial correlation of a variable across a region of interest. Variogram analysis allows for the understanding of the spatial structure of a variable, which is essential for accurate spatial prediction and interpolation, such as kriging.
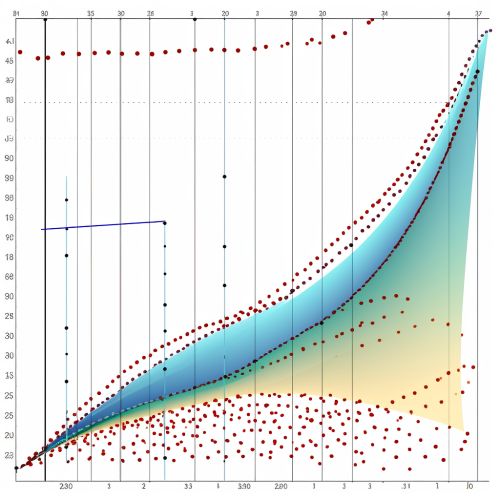
Variogram Function
The variogram function is a measure of the degree of spatial dependence of a spatial random field or stochastic process. It is defined as the variance of the difference between field values at two locations across a variety of scales. Mathematically, the variogram, denoted as γ(h), for a separation distance (or lag) h, is defined as:
- γ(h) = 0.5 * E{[Z(x+h) - Z(x)]^2}
where E denotes the expectation operator, Z(x) is the value of the field at location x, and Z(x+h) is the value of the field at a location h units away from x. The variogram function increases with distance, reflecting the increasing dissimilarity of values as the separation between them increases.
Components of a Variogram
A variogram is typically characterized by three key components: the nugget, the sill, and the range.
Nugget
The nugget, or nugget effect, represents the variance at zero distance, i.e., the variance of differences between values at the same location. It is the y-intercept of the variogram function. The nugget can be interpreted as a measure of the spatial variability at distances smaller than the smallest sampling interval, or as a measure of measurement error.
Sill
The sill is the value at which the variogram function levels off as the separation distance increases. It represents the overall variance in the data set. The difference between the sill and the nugget is the spatially structured variance, which can be modeled and used for spatial prediction.
Range
The range is the distance at which the variogram reaches the sill. It represents the maximum distance at which there is spatial autocorrelation. Beyond the range, the variable is no longer spatially autocorrelated.
Variogram Models
There are several commonly used theoretical models for variograms, including the spherical, exponential, and Gaussian models. These models are used to fit the experimental variogram, which is calculated from the data, in order to predict values at unsampled locations.
Spherical Model
The spherical model is the most commonly used variogram model. It is characterized by a linear increase from the nugget to the range, and a constant sill beyond the range.
Exponential Model
The exponential model is characterized by a rapid increase from the nugget and a gradual approach to the sill. It does not reach the sill within the range, but instead asymptotically approaches it.
Gaussian Model
The Gaussian model is characterized by a very slow increase from the nugget and a rapid increase to the sill near the range. It is often used when there is a high degree of spatial autocorrelation.
Applications of Variogram Analysis
Variogram analysis is widely used in various fields such as geology, hydrology, ecology, and atmospheric science. It is used for spatial prediction, spatial interpolation, and spatial uncertainty quantification. It is also used in the design of optimal sampling strategies, as it provides information about the spatial structure of the variable of interest.
