Kriging
Introduction
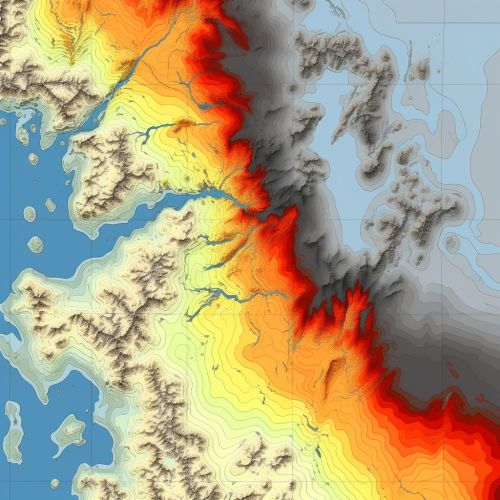
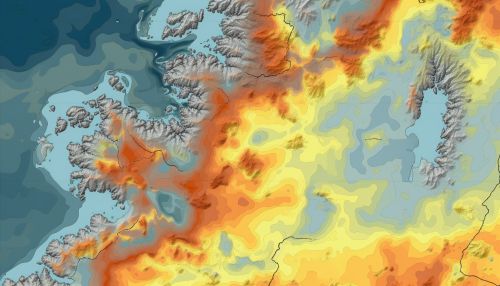
Kriging is a group of statistical techniques used in the field of Geostatistics to interpolate the value of a random field at an unobserved location from observations of its value at nearby locations. Named after South African mining engineer Danie G. Krige, Kriging or Gaussian process regression is a method of interpolation that assumes the distance or direction between sample data points reflects a spatial correlation that can be used to explain variation in the field.


History
Kriging was developed in the field of Mining engineering in the 1950s. The technique was named after Danie G. Krige, a South African mining engineer who sought to predict the most likely distribution of valuable minerals in a mine based on samples taken from a small number of boreholes. Krige's work was later formalized by French mathematician Georges Matheron in the 1960s, who is considered the founder of the field of geostatistics.
Theory
The theoretical basis of Kriging lies in the field of Stochastic processes. The method assumes that the distance or direction between sample points reflects a spatial correlation that can be used to explain variation in the field. This correlation is often calculated using a Semivariogram, which measures the variance between data points as a function of distance.

Types of Kriging
There are several types of Kriging, including Simple Kriging, Ordinary Kriging, Universal Kriging, and Co-Kriging.
Simple Kriging
Simple Kriging assumes a known, constant mean value across the entire field. This method is rarely used in practice as it is unlikely that the mean would be known or constant across the entire field.
Ordinary Kriging
Ordinary Kriging assumes a constant but unknown mean. It is the most commonly used form of Kriging due to its flexibility and robustness.
Universal Kriging
Universal Kriging, also known as Kriging with a trend, assumes a non-constant mean that can be modeled by a polynomial function.
Co-Kriging
Co-Kriging is a multivariate form of Kriging that uses information from correlated variables to improve the estimation of the primary variable of interest.
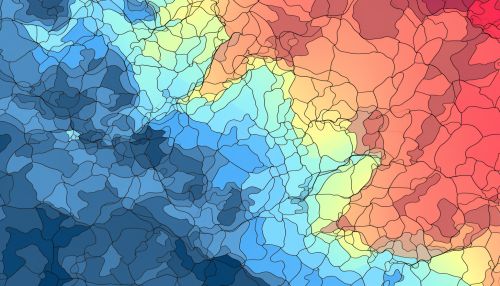
Applications
Kriging has a wide range of applications in various fields such as Geology, Meteorology, Hydrology, Geography, and Soil science. It is used to create contour maps of geographic variables, to predict weather patterns, to estimate soil properties, and to model the spread of pollutants or diseases.
Limitations and Assumptions
Kriging makes several assumptions that may not hold true in all cases. These include stationarity (the statistical properties of the field are the same everywhere), isotropy (the statistical properties are the same in all directions), and the absence of trends. Furthermore, Kriging is sensitive to the choice of the semivariogram model and parameters.