Trilateration
Introduction
Trilateration is a mathematical technique used for determining the intersections of three sphere surfaces given the centers and radii of the three spheres. In two-dimensional geometry, it is used to determine the location of a point based on the distances to three known points. This technique is commonly used in navigation, geophysics, and in positioning systems such as GPS.


Principle
The principle of trilateration is based on the properties of circles, spheres, and triangles. In a two-dimensional plane, if the distances from a point to three known points are given, the location of the point can be determined by finding the intersection of the three circles centered at the known points with radii equal to the given distances. In three dimensions, the process is similar, but spheres are used instead of circles.
Mathematical Background
Trilateration involves solving the equations of three spheres (in three dimensions) or circles (in two dimensions) for their intersection points. The equations of the spheres or circles are derived from the Pythagorean theorem, which states that in a right triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides.
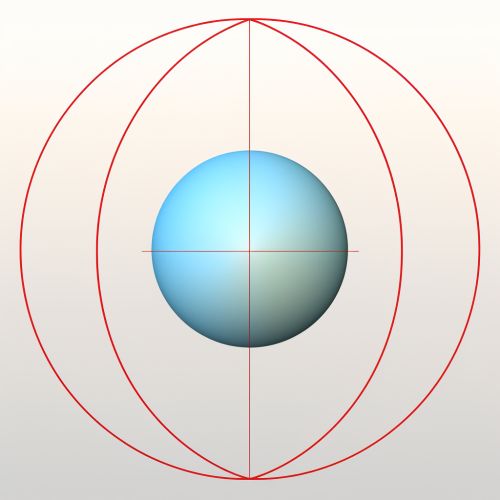
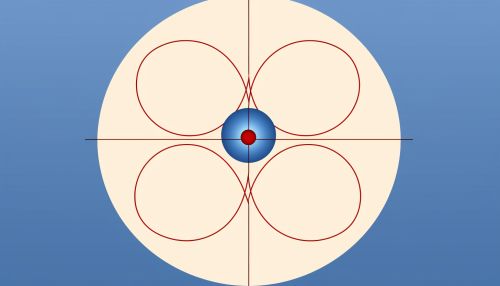
Applications
Trilateration has a wide range of applications in various fields. Some of the most common applications include:
Trilateration is a fundamental principle used in navigation systems, including GPS. In GPS, the location of a receiver can be determined by measuring the distances to at least three satellites and then using trilateration to find the intersection point of the spheres centered at the satellites.
Geophysics
In geophysics, trilateration is used to determine the location of seismic events. By measuring the time it takes for seismic waves to reach three different seismometers, the location of the event can be determined.
Computer Networking
In computer networking, trilateration can be used to determine the location of a device in a wireless network. By measuring the signal strength at three different points, the location of the device can be determined.


Limitations and Challenges
While trilateration is a powerful tool, it is not without its limitations and challenges. Some of these include:
Accuracy
The accuracy of trilateration is dependent on the accuracy of the distance measurements. If the distances are not measured accurately, the calculated location will not be accurate.
Geometry
The geometry of the known points can affect the accuracy of trilateration. If the known points are too close together or in a straight line, the intersection point may not be well defined.
Noise
In real-world applications, noise can affect the distance measurements, leading to errors in the calculated location.


Conclusion
Trilateration is a fundamental mathematical technique with wide-ranging applications in fields such as navigation, geophysics, and computer networking. Despite its limitations and challenges, it remains an essential tool in these and many other areas.
