Pearson correlation coefficient
Introduction
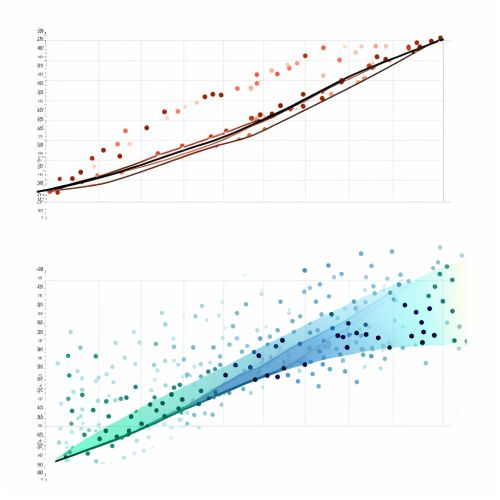
The Pearson correlation coefficient, also referred to as Pearson's r, the Pearson product-moment correlation coefficient (PPMCC), or the bivariate correlation, is a measure of the linear correlation between two variables X and Y. It has a value between +1 and −1. A value of +1 is total positive linear correlation, 0 is no linear correlation, and −1 is total negative linear correlation. It is widely used in the sciences as a measure of the degree of linear dependence between two variables.
Mathematical Definition
The Pearson correlation coefficient is defined as the covariance of the two variables divided by the product of their standard deviations. This can be represented mathematically as:
ρ(X,Y) = cov(X,Y) / (σX * σY)
Where: ρ(X,Y) is the Pearson correlation coefficient of X and Y, cov(X,Y) is the covariance between X and Y, σX is the standard deviation of X, σY is the standard deviation of Y.
The Pearson correlation coefficient is symmetric: the correlation of X and Y is the same as the correlation of Y and X.
Properties
The Pearson correlation coefficient possesses several important properties. These include:
- It is invariant under separate changes in location and scale in the two variables. This means that multiplying all values of one variable by a constant, or adding a constant to all values, does not change the coefficient.
- The absolute value of the Pearson correlation coefficient gives the size of the linear relationship between the variables. A value of 1 means a perfect positive correlation and a value of -1 means a perfect negative correlation.
- The sign of the Pearson correlation coefficient indicates the direction of the association. If both variables tend to increase or decrease together, the coefficient is positive, and if one variable tends to increase as the other decreases, the coefficient is negative.
- The square of the Pearson correlation coefficient, often denoted r², is the proportion of the variance in the two variables that is predictable from the other.
Calculation
The Pearson correlation coefficient is calculated as the ratio of the summed product of the mean-adjusted values of the two variables, to the square root of the product of the summed squares of the mean-adjusted values of each variable. This can be represented mathematically as:
r = Σ((xi - μx)(yi - μy)) / √[ Σ(xi - μx)² * Σ(yi - μy)² ]
Where: xi and yi are the individual sample points indexed with i, μx and μy are the means of x and y respectively.
Interpretation
The Pearson correlation coefficient is a measure of the strength and direction of association that exists between two continuous variables. The value of r is always between +1 and –1. To interpret its value, the following guide gives a rough view:
- 0.00-0.19 “very weak”
- 0.20-0.39 “weak”
- 0.40-0.59 “moderate”
- 0.60-0.79 “strong”
- 0.80-1.0 “very strong”
Limitations
While the Pearson correlation coefficient is a powerful tool, it does have limitations. These include:
- It only measures linear relationships: If the relationship is not linear, Pearson's correlation coefficient may be misleading.
- It is sensitive to outliers: Outliers can have a large effect on the Pearson correlation coefficient, skewing the results.
- It does not imply causation: A high Pearson correlation coefficient does not mean that one variable causes the other to change. Correlation does not imply causation.
Applications
The Pearson correlation coefficient is used in a wide variety of fields. These include:
- In statistics, where it provides a measure of the strength and direction of a linear relationship between two random variables.
- In psychology, where it is used to measure the strength of association between two variables.
- In finance, where it is used to measure the degree of relationship between two stocks or financial instruments.
- In biology, where it is used to measure the degree of relationship between two biological variables.
