Vector Field

Definition

A vector field is a mathematical concept that assigns a vector to every point in a subset of space. In the context of differential geometry, where the concept originated, a vector field on a manifold is a smooth map that takes any point of the manifold to a tangent vector at that point. This is more precisely termed a tangent vector field.

Introduction

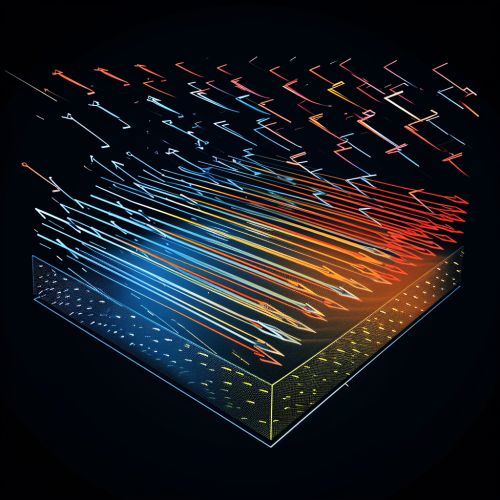
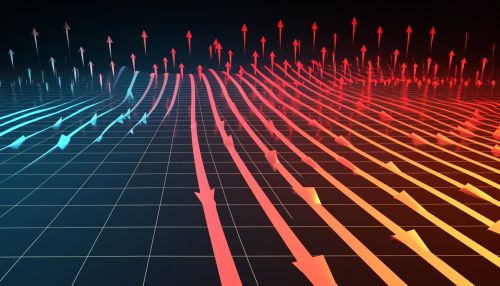
Vector fields are often visualized as arrows that are placed on points in the space, with the direction of the arrow representing the direction of the vector, and the length of the arrow representing the magnitude of the vector. This visualization can be particularly useful in the physical sciences, where vector fields are used to model various phenomena such as electric fields, magnetic fields, and fluid flows.

Mathematical Formalism

In mathematics, a vector field is typically defined on a subset of a R^n or on a manifold. The elements of the vector field are vectors, which are represented as arrows pointing in the direction of the vector. The magnitude of the vector is represented by the length of the arrow.

Types of Vector Fields

There are several types of vector fields, each with their own unique properties and applications. These include:

Gradient Fields

A gradient field is a vector field that is the gradient of a scalar function. This means that at each point in the space, the vector field points in the direction of greatest rate of increase of the scalar function, and its magnitude is the rate of change in that direction.

Divergence-Free Fields

A divergence-free field, also known as a solenoidal field, is a vector field whose divergence is zero at every point in the space. This property is often associated with conservation laws, as it implies that there is no net source or sink of the field at any point.

Curl-Free Fields

A curl-free field, also known as an irrotational field, is a vector field whose curl is zero at every point in the space. This property is often associated with potential fields, as it implies that the field can be expressed as the gradient of a potential function.

Applications

Vector fields have a wide range of applications in various fields of science and engineering. Some of the most common applications include:

Physics

In physics, vector fields are used to describe physical quantities that have both a magnitude and a direction at each point in space. Examples include electric fields, magnetic fields, and gravitational fields.

Engineering

In engineering, vector fields are used in the analysis and design of systems that involve fluid flow, heat transfer, and electromagnetic fields.

Computer Graphics

In computer graphics, vector fields are used to simulate natural phenomena such as wind, water currents, and fire.