Morse Function
Introduction
A Morse function is a type of function used in differential topology, named after mathematician Marston Morse. Morse functions are used to study the topology of manifolds using real-valued smooth functions. They are a fundamental tool in the field of Morse theory, which provides a bridge between the algebraic and geometric aspects of topology.
Definition
In formal terms, a Morse function is a smooth function f from a manifold M to the real numbers R that has only non-degenerate critical points. This means that for any critical point x of f, the Hessian matrix of second derivatives of f at x is non-singular. In other words, its determinant is not zero.
Critical Points and Indices
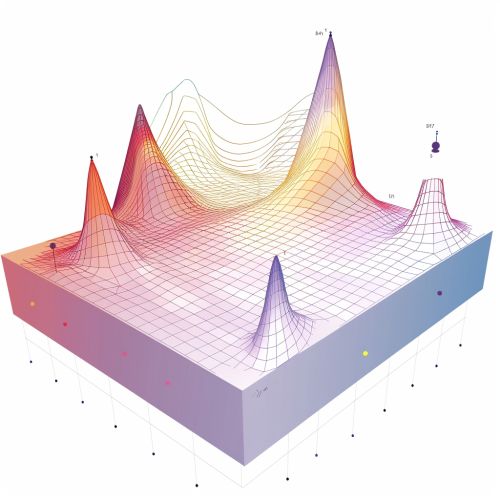
The critical points of a Morse function are the points where the gradient of the function is zero. The index of a critical point is defined as the number of negative eigenvalues of the Hessian matrix at that point. This index gives us important information about the local behavior of the function near the critical point. For example, a critical point with index 0 is a local minimum, a critical point with index 1 is a saddle point with one downward direction, and so on.
Morse Theory
Morse theory is a branch of differential topology that studies the relationships between the critical points of a Morse function and the topology of the manifold on which it is defined. It was developed by Marston Morse in the 1920s and 1930s. The main result of Morse theory is that the topology of a manifold can be determined by examining the critical points of a Morse function defined on the manifold. This leads to a powerful method for studying the topology of manifolds and has many applications in mathematics and physics.
Applications
Morse functions and Morse theory have wide-ranging applications in various fields of mathematics and physics. In mathematics, they are used in areas such as algebraic topology, differential geometry, and dynamical systems. In physics, they are used in the study of Hamiltonian systems, quantum field theory, and string theory.
See Also
- Differential topology
- Algebraic topology
- Differential geometry
- Dynamical systems
- Hamiltonian systems
- Quantum field theory
- String theory