Logistic growth
Introduction
Logistic growth is a concept in population ecology that describes how the size of a population changes over time in a limited environment. It is a model that exhibits the property of saturation, where the growth rate decreases as the population approaches the carrying capacity of the environment.
Mathematical Description
The logistic growth model is mathematically represented by the differential equation:
\[ \frac{dP}{dt} = rP \left(1 - \frac{P}{K}\right) \]
where:
- P is the population size,
- t is time,
- r is the intrinsic growth rate of the population, and
- K is the carrying capacity of the environment.
The solution to this differential equation is given by the logistic function:
\[ P(t) = \frac{K}{1 + \left(\frac{K - P_0}{P_0}\right)e^{-rt}} \]
where P_0 is the initial population size.
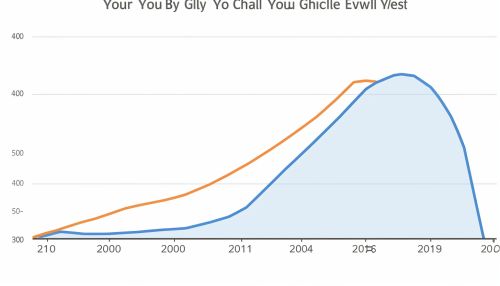
Characteristics of Logistic Growth
Logistic growth is characterized by three distinct phases:
1. Lag phase: This is the initial phase where the population size is small, and growth is slow due to the low number of individuals capable of reproduction.
2. Exponential phase: As the population size increases, the growth rate also increases, leading to a rapid expansion of the population. This phase is characterized by a positive and maximum slope on the logistic growth curve.
3. Saturation phase: As the population size approaches the carrying capacity of the environment, the growth rate decreases due to limited resources, leading to a stabilization of the population size.
Applications of Logistic Growth
Logistic growth models are widely used in various fields such as ecology, economics, and sociology.
In ecology, they are used to model the population dynamics of species living in a limited environment. In economics, they can model the spread of new technologies or the growth of companies. In sociology, they can model the spread of ideas or trends within a society.
Limitations of Logistic Growth
While the logistic growth model is useful in many situations, it has its limitations. It assumes that the carrying capacity is constant, which is not always the case in real-world scenarios. The model also assumes that all individuals in the population are identical and have the same probability of reproducing, which is often not the case.
