Graph Realization Problem

Introduction

The Graph Realization Problem is a fundamental question in graph theory and combinatorics, which seeks to determine whether a given sequence of integers can be realized as the degree sequence of a simple graph. This problem is also known as the Degree Sequence Problem or the Havel-Hakimi Problem, named after the mathematicians Václav Havel and S. L. Hakimi who made significant contributions to its understanding.

A simple graph with vertices labeled with their degrees.

A simple graph with vertices labeled with their degrees.

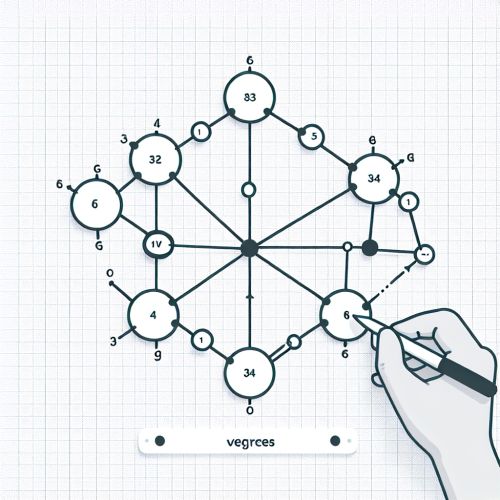
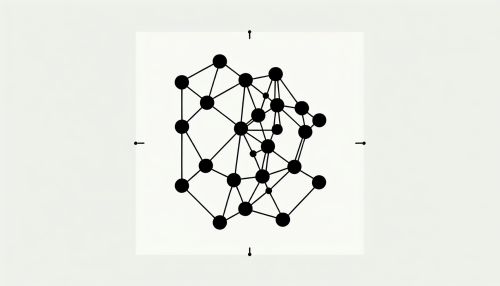
Problem Definition

The Graph Realization Problem can be formally defined as follows: Given a sequence of non-negative integers (d1, d2, ..., dn), does there exist a simple graph with n vertices such that the degree of the i-th vertex is di for all 1 ≤ i ≤ n? A sequence that can be realized as the degree sequence of a simple graph is called a graphical sequence.

Historical Background

The Graph Realization Problem has a rich history dating back to the early 20th century. The first significant result in this area was obtained by the Hungarian mathematician Dénes Kőnig in 1927. He proposed a necessary and sufficient condition for a sequence to be graphical, which is now known as Kőnig's Theorem.

Kőnig's Theorem

Kőnig's Theorem states that a sequence (d1, d2, ..., dn) of non-negative integers is graphical if and only if the sum of the sequence is even and the sum of the largest d1 elements is less than or equal to d1 + the sum of the next d2 elements + ... + dn for all 1 ≤ i ≤ n.

Havel-Hakimi Algorithm

In 1962, Havel and Hakimi independently proposed a simple and efficient algorithm to solve the Graph Realization Problem. The Havel-Hakimi algorithm is based on the idea of repeatedly removing the highest degree vertex and reducing the degrees of its neighbors.

Applications

The Graph Realization Problem has numerous applications in various fields such as computer science, operations research, and social network analysis. It is used in the design of networks, the analysis of molecular structures in chemistry, and the study of social structures, among others.

Open Problems

Despite the significant progress made in understanding the Graph Realization Problem, several intriguing questions remain open. For example, it is still unknown whether there exists a polynomial-time algorithm for the Graph Realization Problem in the case of multigraphs.

See Also

• Erdős–Gallai theorem
• Handshaking lemma
• Graph (discrete mathematics)