Hermite polynomials: Difference between revisions
(Created page with "== Introduction == Hermite polynomials are a classical orthogonal polynomial sequence that arise in probability, combinatorics, and numerical analysis. They are named after the French mathematician Charles Hermite (1822–1901). These polynomials are solutions to the Hermite differential equation and are used in various fields such as quantum mechanics, particularly in the context of the quantum harmonic oscillator. == Definition == The Hermite polynomials \( H_n(x) \)...") |
No edit summary |
||
| Line 46: | Line 46: | ||
== Visualization == | == Visualization == | ||
[[Image:Detail-93369.jpg|thumb|center|Graph of the first few Hermite polynomials.|class=only_on_mobile]] | |||
[[Image:Detail-93370.jpg|thumb|center|Graph of the first few Hermite polynomials.|class=only_on_desktop]] | |||
== See Also == | == See Also == | ||
Latest revision as of 10:13, 22 June 2024
Introduction
Hermite polynomials are a classical orthogonal polynomial sequence that arise in probability, combinatorics, and numerical analysis. They are named after the French mathematician Charles Hermite (1822–1901). These polynomials are solutions to the Hermite differential equation and are used in various fields such as quantum mechanics, particularly in the context of the quantum harmonic oscillator.
Definition
The Hermite polynomials \( H_n(x) \) can be defined in several equivalent ways. One common definition is through the Rodrigues' formula: \[ H_n(x) = (-1)^n e^{x^2} \frac{d^n}{dx^n} e^{-x^2} \] where \( n \) is a non-negative integer.
Another definition involves the generating function: \[ e^{2xt - t^2} = \sum_{n=0}^{\infty} H_n(x) \frac{t^n}{n!} \]
Orthogonality
Hermite polynomials are orthogonal with respect to the weight function \( e^{-x^2} \) on the entire real line. This orthogonality can be expressed as: \[ \int_{-\infty}^{\infty} H_m(x) H_n(x) e^{-x^2} \, dx = \sqrt{\pi} 2^n n! \delta_{mn} \] where \( \delta_{mn} \) is the Kronecker delta, which is 1 if \( m = n \) and 0 otherwise.
Recurrence Relations
Hermite polynomials satisfy the following recurrence relations: \[ H_{n+1}(x) = 2x H_n(x) - 2n H_{n-1}(x) \] \[ \frac{d}{dx} H_n(x) = 2n H_{n-1}(x) \]
Differential Equation
Hermite polynomials are solutions to the Hermite differential equation: \[ y - 2xy' + 2ny = 0 \] where \( y = H_n(x) \).
Properties
Hermite polynomials have several important properties:
- **Symmetry**: \( H_n(-x) = (-1)^n H_n(x) \)
- **Normalization**: \( H_n(0) = (-1)^{n/2} \frac{n!}{(n/2)!} \) if \( n \) is even, and 0 if \( n \) is odd.
- **Asymptotic Behavior**: For large \( n \), \( H_n(x) \) behaves asymptotically as \( H_n(x) \sim 2^n x^n \).
Applications
Hermite polynomials are used in various applications, including:
- **Quantum Mechanics**: In the solution of the quantum harmonic oscillator, the wave functions are expressed in terms of Hermite polynomials.
- **Probability Theory**: In the context of the Gaussian distribution, Hermite polynomials appear in the Edgeworth series, which approximates probability distributions.
- **Numerical Analysis**: Hermite interpolation uses Hermite polynomials to construct polynomial approximations that match function values and derivatives at given points.
Example Polynomials
The first few Hermite polynomials are:
- \( H_0(x) = 1 \)
- \( H_1(x) = 2x \)
- \( H_2(x) = 4x^2 - 2 \)
- \( H_3(x) = 8x^3 - 12x \)
- \( H_4(x) = 16x^4 - 48x^2 + 12 \)
Visualization
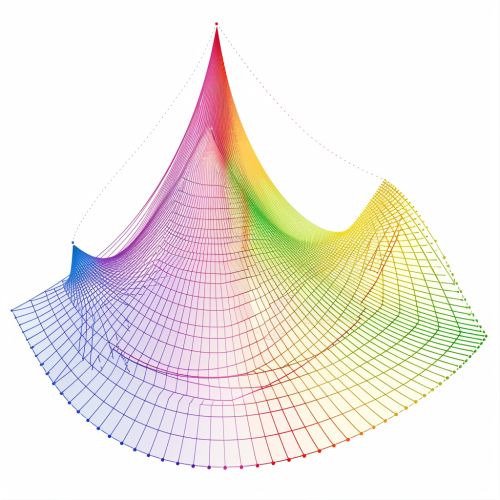
See Also
References
- Szegő, Gábor. "Orthogonal Polynomials." American Mathematical Society, 1939.
- Arfken, George B.; Weber, Hans J. "Mathematical Methods for Physicists." Academic Press, 2005.
