Instantaneous rate of change

Introduction

The instantaneous rate of change is a fundamental concept in calculus and mathematical analysis, representing the rate at which a quantity changes at a specific instant. This concept is crucial in various fields such as physics, engineering, economics, and biology, where it is used to model and analyze dynamic systems. The instantaneous rate of change is mathematically defined as the derivative of a function at a particular point.

Definition and Mathematical Formulation

The instantaneous rate of change of a function \( f(x) \) at a point \( x = a \) is defined as the limit of the average rate of change as the interval approaches zero. Mathematically, it is expressed as:

\[ f'(a) = \lim_Template:H \to 0 \frac{f(a+h) - f(a)}{h} \]

This limit, if it exists, is called the derivative of \( f \) at \( a \), denoted by \( f'(a) \). The derivative represents the slope of the tangent line to the graph of the function at the point \( (a, f(a)) \).

Geometric Interpretation

Geometrically, the instantaneous rate of change at a point corresponds to the slope of the tangent line to the curve of the function at that point. If the function \( f(x) \) is plotted on a Cartesian plane, the tangent line at \( x = a \) touches the curve at exactly one point and has the same slope as the curve at that point.

A graph showing a curve with a tangent line touching it at a single point.

A graph showing a curve with a tangent line touching it at a single point.

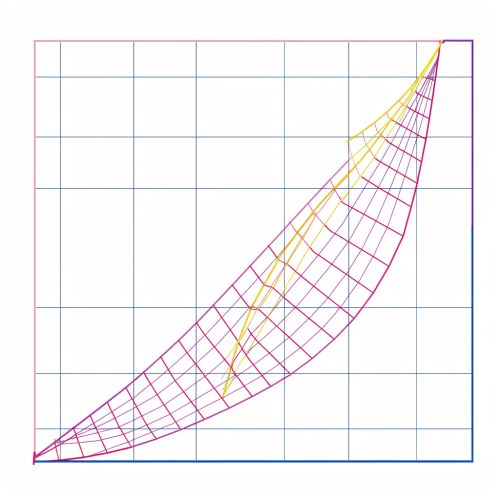
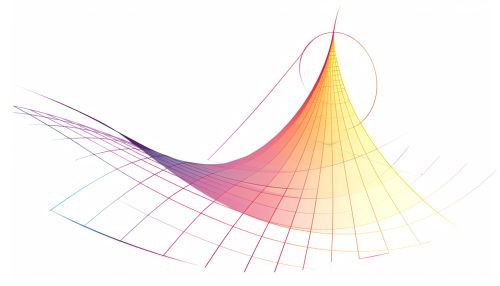
Physical Interpretation

In physics, the instantaneous rate of change is often interpreted as velocity or acceleration. For instance, if \( s(t) \) represents the position of an object as a function of time \( t \), then the instantaneous velocity \( v(t) \) is the derivative of the position function:

\[ v(t) = s'(t) \]

Similarly, the instantaneous acceleration \( a(t) \) is the derivative of the velocity function:

\[ a(t) = v'(t) = s(t) \]

Applications in Various Fields

Physics

In addition to velocity and acceleration, the concept of instantaneous rate of change is used in other areas of physics, such as electromagnetism, where it describes the rate of change of electric and magnetic fields.

Engineering

In engineering, the instantaneous rate of change is used to model and analyze systems that change over time, such as the stress and strain in materials, fluid flow, and thermal dynamics.

Economics

In economics, the instantaneous rate of change is used to analyze the behavior of economic variables, such as the rate of change of cost, revenue, and profit functions. For example, the marginal cost is the instantaneous rate of change of the total cost function with respect to the quantity of output.

Biology

In biology, the instantaneous rate of change is used to model population growth, the spread of diseases, and other dynamic processes in biological systems.

Higher-Order Derivatives

The concept of the instantaneous rate of change can be extended to higher-order derivatives. The second derivative of a function \( f(x) \), denoted by \( f(x) \), represents the rate of change of the rate of change, providing information about the concavity of the function. Higher-order derivatives can be used to analyze more complex behaviors of functions.

Techniques for Finding Derivatives

Several techniques are used to find the derivative of a function, including:

Power Rule

For any real number \( n \),

\[ \frac{d}{dx} x^n = nx^{n-1} \]

Product Rule

For two differentiable functions \( u(x) \) and \( v(x) \),

\[ \frac{d}{dx} [u(x)v(x)] = u'(x)v(x) + u(x)v'(x) \]

Quotient Rule

For two differentiable functions \( u(x) \) and \( v(x) \),

\[ \frac{d}{dx} \left[ \frac{u(x)}{v(x)} \right] = \frac{u'(x)v(x) - u(x)v'(x)}{[v(x)]^2} \]

Chain Rule

For two differentiable functions \( f(x) \) and \( g(x) \),

\[ \frac{d}{dx} f(g(x)) = f'(g(x))g'(x) \]

Implicit Differentiation

Implicit differentiation is a technique used to find the derivative of a function defined implicitly by an equation involving both \( x \) and \( y \). For example, if \( F(x, y) = 0 \), then the derivative \( \frac{dy}{dx} \) can be found by differentiating both sides of the equation with respect to \( x \) and solving for \( \frac{dy}{dx} \).

Related Concepts

Differentiability

A function is said to be differentiable at a point if its derivative exists at that point. Differentiability implies continuity, but a continuous function is not necessarily differentiable.

Critical Points

Critical points of a function are points where the derivative is zero or undefined. These points are important in determining the local maxima and minima of the function.

Inflection Points

Inflection points are points where the concavity of the function changes. These points are found by analyzing the second derivative of the function.

See Also

• Derivative
• Tangent (geometry)
• Velocity
• Acceleration
• Marginal cost
• Population dynamics