Polynomial function: Difference between revisions
(Created page with "== Definition and Basic Concepts == A '''polynomial function''' is a function that can be expressed in the form of a polynomial. In mathematics, a polynomial is an expression consisting of variables and coefficients, involving only the operations of addition, subtraction, multiplication, and non-negative integer exponents of variables. The degree of the polynomial is the highest power of the variable in that polynomial, as long as there is only one variabl...") |
No edit summary |
||
| (One intermediate revision by the same user not shown) | |||
| Line 2: | Line 2: | ||
A '''polynomial function''' is a function that can be expressed in the form of a polynomial. In mathematics, a [[Polynomial|polynomial]] is an expression consisting of variables and coefficients, involving only the operations of addition, subtraction, multiplication, and non-negative integer exponents of variables. The degree of the polynomial is the highest power of the variable in that polynomial, as long as there is only one variable. | A '''polynomial function''' is a function that can be expressed in the form of a polynomial. In mathematics, a [[Polynomial|polynomial]] is an expression consisting of variables and coefficients, involving only the operations of addition, subtraction, multiplication, and non-negative integer exponents of variables. The degree of the polynomial is the highest power of the variable in that polynomial, as long as there is only one variable. | ||
[[Image:Detail-77867.jpg|thumb|center|A graph displaying a curve representing a polynomial function.|class=only_on_mobile]] | |||
[[Image:Detail-77868.jpg|thumb|center|A graph displaying a curve representing a polynomial function.|class=only_on_desktop]] | |||
Polynomials appear in a wide variety of areas within mathematics and science. They are used to construct polynomial equations, which encode a wide range of problems, from elementary word problems to complicated problems in the sciences. They are used to interpolate data and to create mathematical models. | Polynomials appear in a wide variety of areas within mathematics and science. They are used to construct polynomial equations, which encode a wide range of problems, from elementary word problems to complicated problems in the sciences. They are used to interpolate data and to create mathematical models. | ||
Latest revision as of 03:44, 8 May 2024
Definition and Basic Concepts
A polynomial function is a function that can be expressed in the form of a polynomial. In mathematics, a polynomial is an expression consisting of variables and coefficients, involving only the operations of addition, subtraction, multiplication, and non-negative integer exponents of variables. The degree of the polynomial is the highest power of the variable in that polynomial, as long as there is only one variable.
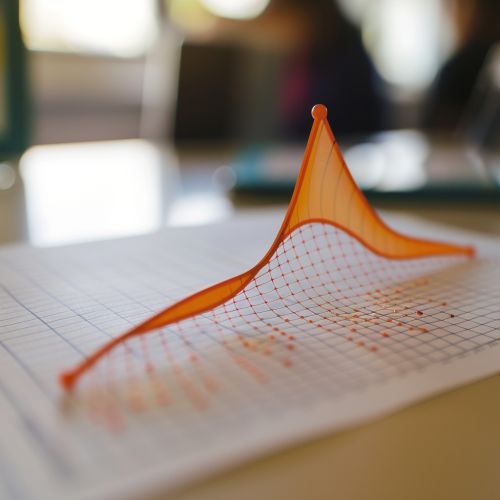
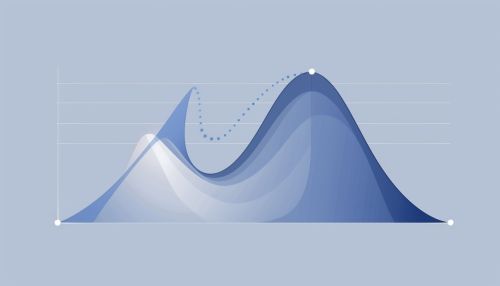
Polynomials appear in a wide variety of areas within mathematics and science. They are used to construct polynomial equations, which encode a wide range of problems, from elementary word problems to complicated problems in the sciences. They are used to interpolate data and to create mathematical models.
Polynomial Functions
In the context of function theory, a polynomial function is a function defined by evaluating a polynomial. More formally, a function f from the real or complex numbers to the real or complex numbers is called a polynomial function if there exists a polynomial p with real or complex coefficients such that for all x in the domain of f, f(x) = p(x).
Properties of Polynomial Functions
Polynomial functions have several properties that make them easy to work with in mathematical analysis. These properties include:
- Continuity: Polynomial functions are continuous, meaning that the graph of a polynomial function has no breaks or holes. This is a consequence of the fact that the operations of addition, subtraction, and multiplication are all continuous.
- Differentiability: Polynomial functions are differentiable, meaning that they have a derivative. The derivative of a polynomial function is another polynomial, and it can be found using the power rule for differentiation.
- End Behavior: The end behavior of a polynomial function refers to the behavior of the graph of the polynomial function as it approaches positive or negative infinity. The end behavior of a polynomial function is determined by the degree and the leading coefficient of the polynomial.
- Roots: The roots of a polynomial function are the values of x for which the function equals zero. These are also the x-intercepts of the graph of the polynomial function. The Fundamental Theorem of Algebra states that a polynomial function of degree n has exactly n roots, although some of these may be repeated or may be complex numbers.
Polynomial Equations
A polynomial equation is an equation in which a polynomial function equals zero. The solutions to a polynomial equation are the roots of the corresponding polynomial function. Polynomial equations are often solved using factoring, the quadratic formula, or polynomial long division.
Polynomial Interpolation
Polynomial interpolation is a method of estimating values between two known values. It is used in a wide variety of applications, including computer graphics, statistical analysis, and numerical solutions to differential equations.
Polynomial Models
Polynomial models are mathematical models that use polynomial functions to describe the behavior of a system. These models are often used in the natural sciences and engineering to describe systems that are not easily described by linear models.
